QC7つ道具のひとつである散布図について解説。
異なる2つの量の関係性を見ることができるので、調べたい対象の増減と関係する要素が見つかれば、改善の手がかりにできるかもしれない。
身近な経営工学視点では、気温変化と販売個数の関係について記載しているので、店舗経営している人にもお勧めだ。
「散布図」とは
2種類のデータの関係をひと目でわかるようにした図。
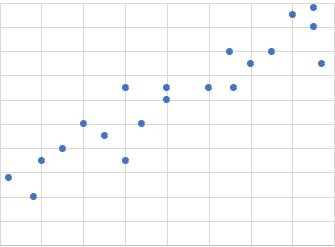
「散布図」をもう少し詳しく
散布図は、横軸と縦軸にそれぞれ別の量を取り、データの当てはまる箇所にプロットした図なので、2種類の量に関係があるか確認するのに役立つ。
あるクラスのテストの点数を散布図にして関係性を見てみよう。
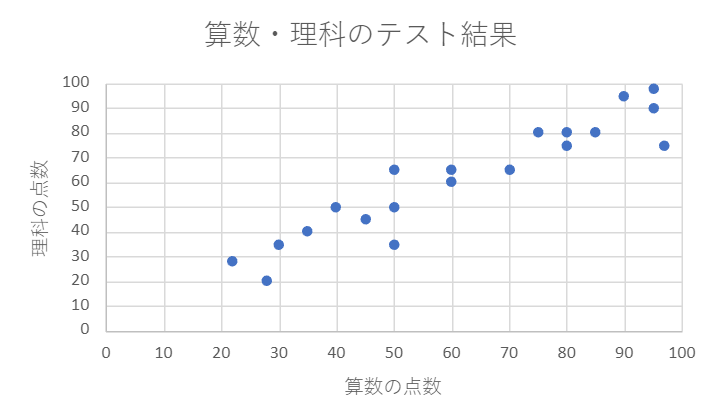
横軸を算数の点数、縦軸を理科の点数としてプロットし散布図を作成した。
この散布図を見ると、算数の成績がよいほど理科の成績もよいという傾向が見えるため、相関関係(一方の数値が増加すると、他方の数値が比例して増加(または減少)する)があると思われる。
ここで注意しなければならないのは、算数と理科の点数には見た目上関係性があるが、因果関係(一方が原因となり他方が発生する)ではないということだ。
分析を行う際は、数値やグラフだけで判断するのではなく、その背景も考察して進めていかなければならない。

「散布図」のパターン
散布図には大きく分けて3つのパターンがある。
●正の相関
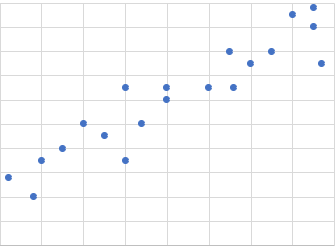
正の相関は、一方が増える時に他方も比例して増える関係だ。
身長と体重の関係などが該当するだろう。
●負の相関
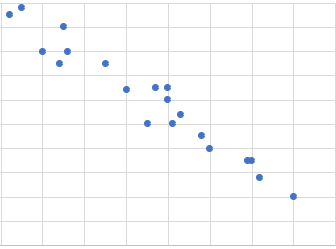
負の相関は、一方が増える時に反比例して減っていく関係だ。
プランクトンの数と海の透明度の関係などが該当するだろう。
●相関なし
2つのデータに関係性が見えない状況だ。
カレーを食べる回数と年収の関係とか。相関あったりして。。
「散布図」のメリットと注意点
散布図のメリットは2つの量的データの関係性がひとめでわかることだ。
散布図を作成してみて、自分の予測した通りに相関性が見つかれば非常に嬉しいし、他者への説明にも役立つだろう。
注意点としては、2つのデータに相関関係がある場合に、因果関係があると判断してはいけないということだ。
見かけ上関係性があっても、2つのデータには間に入る要素があり、その要素とそれぞれ因果関係があるかもしれないからだ。
散布図を作成して予想通り(希望通り)の傾向が見られたとしても、必ず裏を取ることが重要だ。

「散布図」に関する雑記
新人の頃、ある部品の生産パラメータを最適化するのに実験をたくさんやらされて散布図をたくさん作った思い出がある。
散布図を見ると当時のことを思い出して少し悲しい気持ちになるが、散布図のおかげで重要因子を割り出してどうにか乗り切ったと思うと感謝だな。。

「散布図」を身近で活用するなら
天気(主に気温)によって販売個数がどの程度になるか予測する際に役立つので、店舗経営している人にメリットがあるだろう。
天気(主に気温)の予測を基に販売戦略を立てることをウェザーマーチャンダイジングといい、気象庁が研究を行っている。
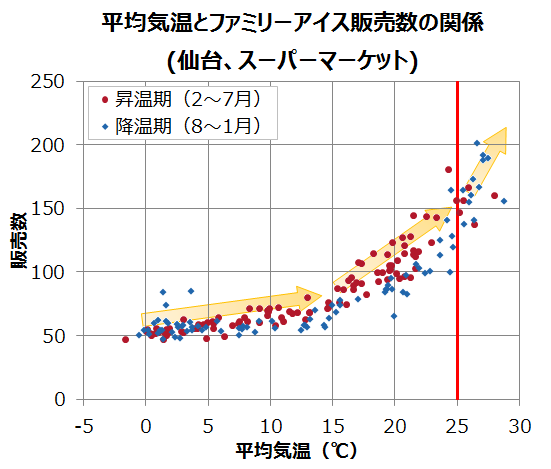
これは仙台のスーパーマーケットにおける7日間平均のファミリーアイスの販売数と平均気温の関係を散布図にしたものだ。
季節に関わらず25度を超えるとアイスの売上が急激に増加していることが分かる。
自社商品の売り上げデータと気温データを突き合せれば、より効率の良い販売促進計画が立てられるかもしれない。
「散布図」のまとめ
散布図は、2種類のデータの関係をひと目でわかるようにした図。
わかるのはあくまで相関関係なので、因果関係ではないことに注意。
身近な経営工学視点では、天気(気温)と販売数の関係分析に応用が可能。



